Universal Superposition of Orthogonal States
The Orthogonal Superposition Machine (or the Quantum Adder) is a quantum machine or protocol which allows creating the superposition of two unknown orthogonal states with the desired weights (absolute values of probability amplitudes) beyond the no-superposition theorem. This task can be done with a higher probability of success than the general superposition protocol. It is also possible to create the superposition of orthogonal qubits with a non-predetermined relative phase with unity probability.
Tags:
Building Blocks, Quantum Functionality, Specific Task, superposition, quantum adder
Assumptions[edit]
The protocol assumes that the input states are unknown and orthogonal to each other.
Outline[edit]
Superposition of arbitrary orthogonal states can be generated with two different types of outputs according to functionality and the desired probability of success. In the first case, a superposition of the two arbitrary states is generated as a pure state with a maximum probability (but not equal to unity) of success. The output state has the well-defined form of the superposition with the desired absolute value and a relative sign of the superposition. In the second case, mixed output state, a superposition with the desired form is successfully generated in all the rounds and thus the success probability of the protocol is equal to one. In this recent case, a mixed state is generated which is the combination of all pure superposed states with different superposition signs and relative phases.
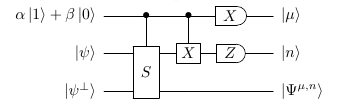
- Pure Output Case: First, an ancillary qubit in standard basis must be prepared with the desired weights of the final superposition. Then the quantum adder circuit must be operated on the two arbitrary and this ancilary qubit. The circuit's gates are as follows: A controlled swap gate acting on input qubits and its control qubit is the ancillary qubit. Then a CNOT gate (controlled X gate) is performed on the first input qubit with the same control qubit. The next step is the measurement. The ancillary qubit is measured in the X basis and the first input state is measured in the Z basis. If the output of the X measurement is the state with positive eigenvalue (or plus state) and the result of the Z measurement is the state with negative eigenvalue (the 1 state) the protocol is successful and the output is the superposition of the two input states with the desired weights. Otherwise, the round should be ignored.
- Mixed Output Case: In the second case, the circuit is the same as for the pure output case. The only difference is that at the measurement step, regardless of the outcome of the measurements, we will not ignore any rounds and all the outcome states are valid superposition but they differ by a relative phase with each other (with negative or positive sign). As a result, the output of the circuit will be always a desired superposed state. In the cases which the relative phase of the superposition can be ignored, this case can be considered as a deterministic protocol.
Notation[edit]
- , : weights of the superposition ()
- : initial states
- : relative non-predetermined phase
- : output superposition of initial orthogonal states in the form of
- : ancillary qubit $|a\rangle = \alpha|1\rangle + \beta |0\rangle$
- : Probability of success of the protocol
Properties[edit]
- Success Claims
- pure output case: In the case with a single pure and positive superposition the success probability of the protocol will be P_{succ} = \frac{1}{2(1+|\alpha||\beta|)}
- mixed output case: In this case, $P_{succ} = 1$ and the described protocol is perfect.
Protocol Description[edit]
Stage 1 Preparation and operation
- Input: The ancillary state , ,
- Output:
- At this stage the following gates will be performed respectively:
- S gate (Controled Swap): Performing this gate will interchange the input qubits. The total states before and after performing this gate are as follows:
- CNOT gate: The total state after this step is as follows:
Stage 2 Measurements
- Input:
- Output: The superposed state
- Measure qubit 1 (the ancilary qubit) in X basis and the qubit 2 in Z basis.
- Pure Output Case:
- if:' The output of the X measurement is 0 AND the output of Z measurement is 1
- Then: Accept the round
- Else: Reject.
- The successful output is in the form:
- Pure Output Case:
is a relative phase which is
- Mixed Output Case:
- Always accept. The protocol is perfect.
- The output will be:, is a relative phase which depends on the outputs of the measurements but in all cases, the superposition has the desired form and weights.
- Mixed Output Case:
Further Information[edit]
- DKK(2017) The above protocol
- OGHW(2016) The first paper that talks about and proves the no-superposition theorem. Also in this paper, they present a probabilistic protocol for superposing two arbitrary (but not completely unknown) states where we know the overlaps of them with a fixed reference state. this protocol, is also restricted to a set of input states.