Probabilistic Cloning
This protocol achieves the functionality of Quantum Cloning. The term Probabilistic Machine identifies that the output copies are exactly identical to the original state but the protocol is not successful in all of the rounds. The probabilistic cloner is not a universal quantum cloning machine and it is limited to a special class of input states. The laws of quantum mechanics allow a probabilistic cloner to make copies from a set of linearly-independent quantum states.
Tags: Non-Universal Cloning, Phase Variant Cloning, State Dependent N-M Cloning Building Blocks, Quantum Cloning, Non-Universal Cloning, copying quantum states, Quantum Functionality, Specific Task, Optimal or Symmetric Cloning
Assumptions[edit]
- We assume that the protocol succeeds with a certain probability and we are able to get the exact copies of the input states.
- The probabilistic quantum cloning machine can only produce exact copies with a positive success probability from a set of quantum input states which are linearly independent.
Outline[edit]
The probabilistic cloning machine is a quantum cloner which is only able to produce copies of a limited set of linearly-dependent states with a probability of success. Despite deterministic protocols which usually consist of performing a unitary transformation, probabilistic cloning protocols are continued by a measurement. Two cases for probabilistic cloning are discussed below, general case and special case of two qubits. The two-qubit case means that our probabilistic machine is able to copy two non-orthogonal qubits efficiently. A probabilistic cloning protocol has three stages: blank or ancillary state preparation, unitary evolution and, measurement. The protocol can be described as follows
- General case: First, an orthonormal set of states should be prepared. These states will be used as ancillary states for the protocol. Then a unitary transformation will take the input states to a superposition(linear combination of quantum states) of a successful two identically copied states and unsuccessful two-qubit states along with probes states to be measured later. The last stage is the measurement. The output is measured in the basis of the ancillary orthonormal states. With some probability of success, the result of the measurement is the desired outcome and the final state collapses to the two identical desired copies. Otherwise, the protocol is aborted.
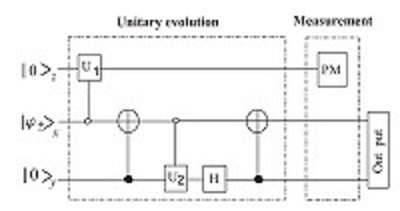
- Two qubit case: This special case is a more practical and clear example of the above general probabilistic cloner. One is only interested in two non-orthogonal qubits to be effectively copied by the probabilistic cloning machine. Here, the orthonormal bases are and . At the first stage of the protocol, only two blank states () are needed. At the second stage, the unitary transformation takes the states to a superposition of two identical states along with the state and a two-qubit state (wrong state) along with the qubit . At the final stage, the third qubit is be measured in basis . If the result of the measurement is the protocol is successful. Otherwise, the round is discarded. This construction can be shown more clearly in the quantum circuit below.
Notation[edit]
- Set of linearly independent states which can be copied by the probabilistic cloning machine
- Input state of the probabilistic cloner
- Set of orthonormal states used as ancillary states for the general probabilistic cloning machine
- The unitary evolution of the quantum cloning machine
- The success probability of the desired copies
- Coefficients of the final state of the output qubits when the protocol fails
- The state of the output qubits when the protocol fails
- The states of the two possible non-orthogonal input qubits which the probabilistic cloner can produce copies of them (two-qubit case)
- The success probability for the two-qubit case
- Unitary gates used in the quantum circuit of the two-qubit probabilistic cloner
- Hadamard gate
Properties[edit]
Success Probability Claims
- General case: The success probability for cloning the elements of the input set of linearly independent states satisfies the following matrix relation:
where ,
,
and
- Two qubits case: The optimal success probability for the probabilistic machine which is able to clone two non-orthogonal qubits is:
Protocol Description[edit]
The probabilistic cloning machine can only perform effectively for a special set of input states. It was shown that states chosen from a set can be probabilistic-ally cloned if and only if the are linearly independent. This protocol in general consists of three stages as follows:
General case[edit]
Stage 1 Ancilla preparation
- Prepare an orthonormal set of states such as where for . These states act as ancillary states of the protocol.
Stage 2 Unitary Evolution
Input: , ,
Output:
- Perform the unitary transformation of the following form:
Stage 3 Measurements
Input:
Output: with probability
- Measure the ancilla states on the basis .
- If The output of the measurement is the state
- Then the protocol is successful and the output is the desired clones.
- Else Abort
Two qubit case[edit]
General Informaton: The special case of the above probabilistic cloning machine is the following protocol for two nonorthogonal qubit states. The input states for this machine are presented in the following form:
where and are two orthogonal bases of a single qubit.
Stage 1 Ancilla preparation
- Prepare two blank states $|0\rangle|0\rangle$. One of these states is the blank state that we will copy on it and the other one is the ancilla.
Stage 2 Unitary Evolution
Input: ,
Output:
- Perform the unitary transformation expressed as:
here we labelled the three qubits by x, y and z
Stage 3 Measurements
Input:
Output: with probabiliy p
- Measure qubit z in the standard basis ( and basis).
- If the output of the measurement is
- Then the protocol is successful and the final state of the machine are
- Else the protocol failed and the final state of the machine is
The quantum circuit[edit]
Finally, the quantum circuit which illustrates the above stages can be described to consist of following gates and parts which have been also shown in the figure in Outline
- Reverse Controlled gate: A controlled unitary gates with the (original) qubit as the control qubit and the qubit as the operational qubit. The unitary gate acts only if the control qubit is . The unitary is:
where the
- A normal CNOT gate: The control qubit is and the operational qubit is (The flip occurs if the control qubit is )
- Reverse Controlled $U_2$ gate: A controlled unitary gates with the (original) qubit as the control qubit and the qubit as the operational qubit. The unitary gate acts only if the control qubit is . The unitary is:
where the
- Hadamard gate: A Hadamard gate on qubit
- Measurement part: Measuring qubit in the standard basis.




























![{\displaystyle C=[c_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc899cd86cd1bda6fcddac654d6a85ab43e5e9b)














![{\displaystyle |\psi _{\pm }\rangle =cos\eta |0\rangle \pm sin\eta |1\rangle ,\quad \eta \in [0,\pi /4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff12ab1bf6721ccbe798c273332a0deecb557dca)









![{\displaystyle \delta =arcsin[({\sqrt {\frac {2}{1+tan^{4}\eta }}}+{\sqrt {\frac {2}{1+tan^{-4}\eta }}})/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/256753aad14c58192e2da099b45c1a803debd1bd)