Multipartite Entanglement Verification
This example protocol implement the task of Multipartite entanglement verification in a multinode quantum network. The protocol uses classical communication and measurements of quantum states to verify whether the parties share a GHZ state. We present here a loss tolerant version of the protocol, which doesn't assume that the source of the state nor the parties (except one) are trusted.
It has various application in a setting where at each timestep a source shares a state. Most of the time this state will be verified using this protocol and once in a while it will be used to perform some computation or communication protocol (e.g. Anonymous transmission)
Tags: Entanglement Verification, Multi Party Protocols, GHZ state
Assumptions[edit]
- Network: The network consists of n nodes that are fully identified and completely connected with pairwise authenticated classical channels. Additionally, there is a secure classical broadcast channel.
- Adversarial model: It suffices for one party to be honest. A dishonest party can be in control of the source.
Outline[edit]
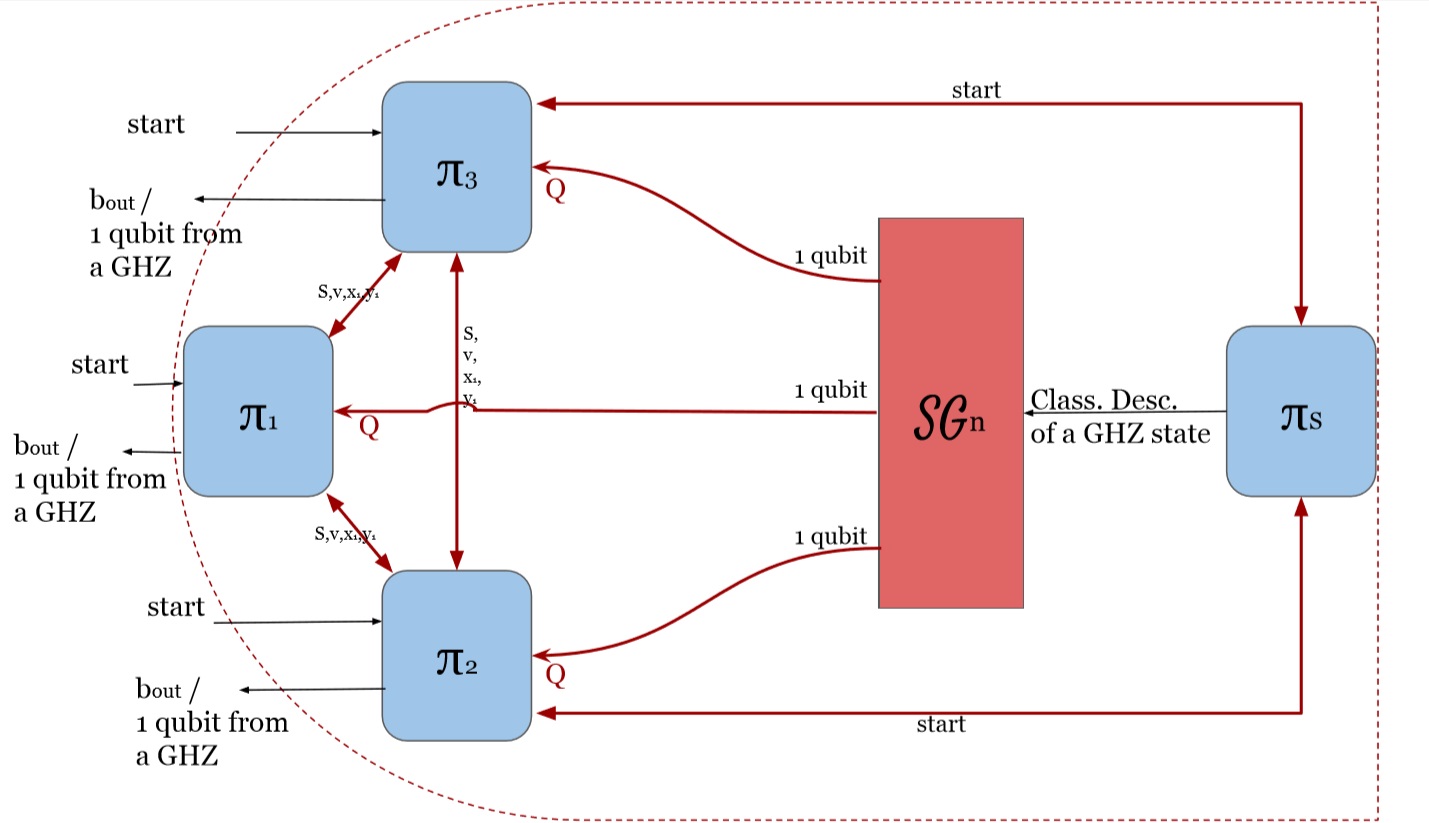
This protocol is based on the work in W. McCutcheon, A. Pappa et al.. The goal is for a specific party called the Verifier to check whether the source has shared a GHZ-state among the n-nodes network. It goes as follow:
- Sharing phase: The source creates and shares an n-qubits quantum state to all the parties using a state generation resource and quantum channels.
- Verification phase: The verifier choses and sends angles to each party that corresponds to measurement basis, using classical authenticated channels. Each party, including the verifier, measures its qubits in the basis indicated by the received angle. It then sends its outcome to the verifier who checks the parity of the outcomes and broadcast if the shared state was a GHZ state.
Notation[edit]
- : Number of parties
- : Identifier of the Verifier
- : Protocol of each party, : Protocol of the verifier, : Protocol of the source
- : n-qubit State Generation resource
- : Angles sent from the Verifier to each party i (indication for the measurement to perform)
- : Rotated measurement basis for the parties.
- : Classical bits sent from each party i to the Verifier (outcome of the measurement)
- : Outcome of the protocol
Requirements[edit]
- Network stage: quantum memory network.
- Authenticated classical channel between the parties
- Quantum channel between the source and the parties
- Ability to perform one-qubit rotation operations and one-qubit measurement at each node
Properties[edit]
- This protocol is correct meaning that if the source shares a GHZ state and every party behaves honestly, the outcome broadcasted by the verifier is .
- The outcome of the protocol directly depends on the trace distance between the shared state and the GHZ state. The output is such that
with and where TD is the trace distance and is a quantum operation acting on the subspace of dishonest parties involved in the protocol (ie a tensor product of an unitary operator on and the identity operator on the rest). This means that the further the shared state is from the GHZ state, the less likely the verifier is going to accept it conditioned on any quantum operation that the dishonest party can locally perform to get closer to the GHZ state.
- This protocol still works in the presence of photon losses.
- This protocol is secure for one round against any coalition of dishonest parties, including the source.
- This protocol is composably secure against a dishonest or noisy source
Pseudo Code[edit]
Protocol for the verifier :
- Input: , 1 qubit, v
- Output: one Bit in and
- Chose randomly angles with such that : is a multiple of
- Upon the reception of the qubit, for send it to party via a private classical channel resource, keep .
- Measures the qubit in the basis and get
- Wait for the reception of all the other .
- Upon the reception of all the , broadcast 0 if and only if
And for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1,...n, i \neq v}
Protocol for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} th party Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_{i}} :
- Input: 1 angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{i}} , 1 qubit and v
- Output: Bit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{i}}
- Wait for the reception of both classical and quantum inputs
- Measures the qubit in the basis
- Send the outcome to the Verifier via the private classical channel resource .
Further Information[edit]
This protocol was first introduced in Multipartite Entanglement Verification Resistant against Dishonest Parties, Anna Pappa et al., in which the authors present an XY version of the protocol where . It means that each party applies an X or a Z gate on its qubit before measuring in the computational basis. It appeared that when a 50% qubit loss rate is tolerated, there exists a cheating strategy allowing a dishonest party to convince the verifier that the state shared was a GHZ state even when it is not. This is why in Experimental verification of multipartite entanglement in quantum networks, W. McCutcheon, A. Pappa et al., the authors present the current version of the protocol which is loss tolerant. They also present an experimental realization of the verification protocol with parties and photonic GHZ states.
In Anonymity for practical quantum networks, Anupama Unnikrishnan et al., Authors use this verification protocol as a subroutine allowing the parties to be certain to have a GHZ state shared when they perform an anonymous transmission protocol.
References[edit]
- Multipartite Entanglement Verification Resistant against Dishonest Parties, Anna Pappa et al., 2012
- Experimental verification of multipartite entanglement in quantum networks, W. McCutcheon, A. Pappa et al., 2016
- Anonymity for practical quantum networks, Anupama Unnikrishnan et al., 2018