Verification of Universal Quantum Computation
Functionality
Quantum Computers perform task which are intractable for classical computers. The basic question here would be, "How should one verify the result of a quantum computer? This task is known as quantum verification or verification of quantum computation. BQP is the class of problems that can be solved by a quantum computer and BPP is the class of problems that can be solved by a classical computer. BPP is contained in BQP and hence, there are problems a quantum computer would solve that are intractable for a classical computer, to put it simply. Thus, if in future, an untrusted company claims to have built a quantum computer, how can the consumer be sure of the correctness of the results when he/she (the consumer) cannot compare the results predicted by the proposed quantum computer? This problem is addressed by the functionality, 'verification of quantum computers'. Verification of universal quantum computation targets every computation that can be performed by a quantum computer.
Tags: Quantum Functionality, Universal Task, Classical Verification of Universal Quantum Computation, Verification of Sub-Universal Quantum Computation, Verification of NP-complete problems
Protocols
- Single-prover prepare-and-send: Verifier can only prepare and send quantum states to delegate a BQP computation to the prover
- Quantum-authentication based verification: Protocols use schemes for authentication of quantum messages to run interactive proofs.
- Trap-based based verification: Protocol uses blind delegated quantum computation
- Verification based on repeated runs
- Single-prover receive-and-measure: Verifier can only receive and measure quantum states
- Measurement only verification: uses blind delegated quantum computation
- Post-hoc verification: Non-interactive (requires only single round of back and forth communication)
- Multi-prover entanglement-based: Verifier is completely classical and the provers are entangled
- Verification based on CHSH rigidity
- Verification based on self-testing graphs
- Post-hoc verification
Properties
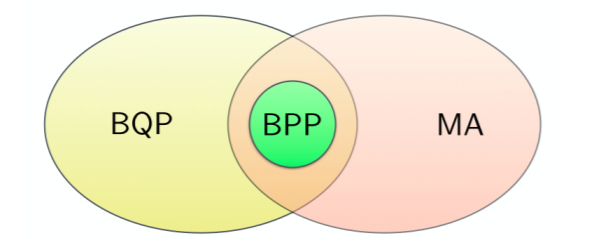
- BQP is the class of problems which can be efficiently solved by quantum computers
- BPP is the class of problems which can be efficiently solved by classical computers.
- MA (Merlin-Arthur) is the class of problems whose solutions can be verified when given a proof setting called witness.
- IP (interactive-proof system) is a generalization of MA, which involves back and forth communication between a verifier (a BPP machine) and prover (has unbounded computational power).
- Protocols 1.1, 1.2 are QPIP protocols and 2.1 is an MIP protocol. QPIP and MIP are classes of decision problems and can be decided by protocols 1.1, 1.2 and 2.1, respectively.
Further Information
This problem remained unsolved for a completely classical client until Urmila Mahadev's protocol for classical verification of quantum protocols in 2018 (See Tags). The problem was formally addressed by Gottesman in 2004, and then promoted by Aaronson in 2007 |(1). Emphasized by Vazirani later in 2007 from a philosophical point of view |(2), he raised the question, 'Is quantum mechanics a falsifiable theory?'
- Review Papers
- Gheorghiu et al (2018): Major portion of this functionality file has been adapted from this review