Prepare and Measure Quantum Digital Signature

Functionality Description

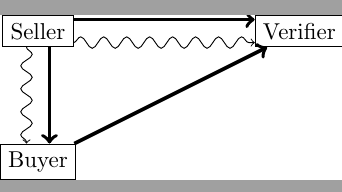
Prepare and Measure QDS achieves the task of Quantum Digital Signature which allows for the exchange of single or multiple bit classical messages from sender to multiple recipients such that parties are required to prepare and measure quantum states instantly without having to store them. For simplicity, most protocols take into account the case of one sender and two recipients (Seller, buyer and verifier) exchanging single-bit classical messages.
It ensures that the sender (seller) cannot deny at a later stage having signed the message, a recipient (buyer) cannot fake or alter the QDS and another sender (verifier) can use the above two properties to verify if the sent message is signed by the genuine sender, thus, satisfying properties of transferability,non-repudiation and unforgeability.

Tags: Multi Party (three), Quantum Enhanced Classical Functionality, Specific Task, Quantum Digital Signature, Quantum Digital Signature with Quantum Memory, Measurement Device Independent Quantum Digital Signature (MDI-QDS), Unconditional Security

Requirements

• Network Stage: Prepare and Measure
• Relevant Network Parameters: $\epsilon _{T},\epsilon _{M}$ (see Prepare and Measure)
• Benchmark values: Transmission distance(d):, Estimated time (t):, QBER(%):

Use Case

Online Transactions, Signing Marksheets

Example:

Outline

---

Quantum Digital Signature (QDS) protocols can be separated into two stages: the distribution stage, where quantum signals (public keys) are sent to all recipients, and the messaging stage, where classical messages are signed, sent and verified. Here, we take the case of three parties, one sender (referred to as seller) and two receivers (buyer and verifier) sharing a one bit message. Distribution phase can be divided into the following steps:

• Key Distribution: Seller generates her (public key,private key) pair and shares the public key with both receivers in this step. For each possible message (0 or 1), she generates two identical sequences/copies (one for each receiver per possible message) of randomly chosen BB84 ∈ {0,1,+,−} states. The sequence of states is called quantum public key and its classical description, private key. She then sends copies of each quantum public key to the receivers while keeping both the private keys secret to herself. At the end of this step, seller has two private keys, one for each possible message. Similarly, each receiver has two quantum public keys, one for each possible message.
• State Elimination: Receivers store their classical records of the quantum public keys in this step. For each quantum public key received, a receiver randomly chooses X or Z basis for each qubit and measures. Whatever outcome he gets, the receiver is certain that seller could not have generated a state orthogonal to his outcome. So, he records the state orthogonal to his outcome as the eliminated signature element. Such measurement is called ’Quantum State Elimination’. The sequence thus generated by measurement of all the qubits in a public key is called receiver’s eliminated signature for the respective quantum public key. Thus, each receiver finally has two eliminated signatures, one for each possible message.
• Symmetrisation: The two receivers exchange half of their randomly chosen eliminated signature elements. This prevents a dishonest seller succeed in cheating by sending dissimilar public keys to the receivers. Thus ends the distribution phase.

$\rightarrow$: Classical channel
~>: Quantum channel

Similarly, Messaging Phase is divided into the following steps:

• Signing: Seller sends desired classical one bit message and the corresponding private key to the desired receiver (called buyer). Buyer compares the private key with his eliminated signature for the corresponding message and counts the number of mismatches (eliminated signature element in seller’s private key).
• Transfer: Buyer forwards the same message and private key to the other receiver (called verifier) who compares it with his eliminated signature for this message.

Properties

---

• The protocol-
  • involves three parties (Seller, Buyer, Verifier) exchanging one-bit classical messages.
  • Requires BB84 QKD setup, authenticated quantum and classical channels
  • assumes maximum number of participating parties are honest. In the present case at least two parties are honest.
  • provides information-theoretic security
  • provides security against repudiation, i.e. the probability that seller succeeds in making buyer and seller disagree on the validity of her sent quantum signature decays exponentially with L, as stated by the formula $P({\text{rep}})\leq e^{-(s_{v}-s_{a})^{2}L}$.
  • provides security against forgery, i.e. any recipient (verifier) with high probability rejects any message which was not originally sent by the seller herself. Forging probability is given by the formula, $P({\text{forge}})\leq e^{-(c_{\min }-2s_{v})^{2}L}$, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\min}} is 3/8 (calculated using uncertainty principle).

Pseudo Code

---

• Notations Used:
  • L: Length of keys used
  • $s_{a}$: Threshold value for signing
  • $s_{v}$: Threshold value for verification
  • $|\psi ^{k}\rangle$: Quantum Public key for message k
  • $\{\beta _{1}^{k},...,\beta _{L}^{k}\}$: Classical Private key for classical one-bit message k
  • $\beta _{l}^{k}$: Classical description of $l^{th}$ qubit in $|\psi ^{k}\rangle$
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^m} : Buyer's Eliminated Signature for message m
  • $V^{m}$: Verifier's Eliminated Signature for message m
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b^k_l} : Buyer’s random bit to determine the measurement basis of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l^{th}} qubit in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi^k\rangle}
  • $v_{l}^{k}$: Verifier’s random bit to determine the measurement basis of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l^{th}} qubit in $|\psi ^{k}\rangle$
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{b^k_l}} : measurement outcome of $b_{l}^{k}$

Stage 1 Distribution

• Input L
• Output Seller: $\{\beta _{1}^{0},...,\beta _{L}^{0}\},\{\beta _{1}^{1},...,\beta _{L}^{1}\}$; Buyer: $B^{0},B^{1}$; Verifier: $V^{0},V^{1}$
  • Key Distribution:

1. For k = 0,1
   1. Seller prepares quantum public key $|\psi ^{k}\rangle =\bigotimes _{l=1}^{L}|\beta _{l}^{k}\rangle$, where $\beta _{l}^{k}\in _{R}\{0,1,+,-\}$
   2. She sends Buyer (k,$|\psi ^{k}\rangle$)
   3. She sends Verifier (k,$|\psi ^{k}\rangle$)

• • State Elimination:

1. For k = 0,1
   1. For l = 1,2,...,L
      1. Buyer chooses $b_{l}^{k}\epsilon _{R}{0,1}$
      2. If $b_{l}^{k}=0$, Buyer measures his qubit in X basis $\{|+\rangle ,|-\rangle \}$
      3. If $b_{l}^{k}=0$, Buyer measures his qubit in Z basis $\{|0\rangle ,|1\rangle \}$
      4. return $m_{b_{l}^{k}}$
      5. $B_{l}^{k}=1-m_{b_{l}^{k}}$

• • Verifier repeats steps 2(a)-2(b) with randomly chosen basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^k_l} to get his eliminated signature elements $V_{l}^{k}$

• • Symmetrisation

1. 1. For k = 0,1
      1. Buyer chooses I$\subset _{R}\{1,2,...,L\},|I|=[L/2]$
      2. $\forall i\epsilon I$, Buyer sends Verifier $(k,i,b_{i}^{k},B_{i}^{k})$
      3. Verifier chooses J$\subset _{R}\{1,2,...,L\},|J|=[L/2]$
      4. $\forall j\epsilon J$, Verifier sends Buyer $(k,j,v_{j}^{k},V_{j}^{k})$
      5. $\forall j\epsilon J$ Buyer replaces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^k_l=V^k_l}
      6. $\forall i\epsilon I$ Verifier replaces $V_{l}^{k}=B_{l}^{k}$

Stage 2 Messaging

• Input Seller: Message m, Private Key for m: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\beta^m_1,...,\beta^m_L\}}
• Output Buyer: accept or abort, Verifier: accept or abort
  • Signing: ’mismatch’ is when Buyer finds an eliminated signature element in Seller’s private key

1. Seller sends Buyer (m,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\beta^m_1,...,\beta^m_L\}} )
2. For l = 1,2,..,L
   1. Buyer counts the number of mismatches ($B_{l}^{m}=V_{l}^{m}$) and returns $S_{b}$
3. If $S_{b}<s_{a}L/2$, Buyer accepts m else he aborts

• • Transfer

1. Buyer sends Verifier (m,$\{\beta _{1}^{m},...,\beta _{L}^{m}\}$)
2. For l = 1,2,....,L
   1. Verifier counts the number of mismatches ($V_{l}^{m}=B_{l}^{m}$) and returns $S_{v}$
3. If $S_{v}<s_{v}L/2$, Verifier accepts m else he aborts

Relevant Papers

Theoretical Papers

1. WDKA (2015) above example
2. DWA (2013) first QDS scheme without quantum memory based on Coherent State Comparison.
   1. Requires Coherent States, authenticated quantum and classical channels, multiports, Unambiguous State Discrimination (USD) (State Elimination), no symmetrisation required.
   2. Security: Information-theoretic
3. AL (2014) establishes coherent state mapping of (2). Replaces SWAP Test with beam splitters. Uses Unambiguous State Discrimination (USD) (State Elimination).
   1. Requires Phase encoded Coherent states, Balanced Beam Splitters.
   2. No explicit security proof provided.
4. AWA (2015) security proof for generalisation of WDKA (2015) and DWA (2013) to more than two recipients case.
5. YFC (2016) first QDS scheme without authenticated (trusted) quantum channels. Demonstrates one protocol with two implementation, two copies of single photon method and decoy state method. First uses single qubit photons in three bases; Private key: classical description of states, Public key: pair of non-orthogonal states in any two of the three bases.
   1. Requires authenticated classical channels, polarisation measurement in three bases, Unambiguous State Discrimination (USD) (State Elimination), uses quantum correlations to check authentication. Decoy State method uses phase-randomised weak coherent states, 50:50 Beam Splitter (BS).
   2. Security: Information-theoretic.
6. AWKA (2015) QDS scheme without authenticated quantum channels using parameter estimation phase. Uses a Key Generation Protocol (KGP) where noise threshold for Seller-Buyer and Seller-Verifier is better than when distilling secret key from QKD. Seller sends different key to Buyer and Verifier using KGP. This anamoly is justifiable due to symmetrisation.
   1. Requires authenticated classical channels, Decoy State QKD setup.
   2. Security: Information-theoretic.
7. WCRZ (2015) demonstrates sending multi-bit classical messages using AWKA (2015) or other similar protocols.
   
8. MH (2016) security proof for generalisation of AWKA (2015) to more than two recipients case.

Experimental Papers

1. CDDWCEJB (2014) first experimental demostartion of a QDS scheme without quantum memory, implements a variant of DWA (2013). Uses unambiguous state elimination (USE) instead of unambiguous state determination (USD)
   1. Per half-bit message: rate=1.4 bits per second, security bound=0.01%, Length of the key (L)= $10^{13}$
2. DCKAWDJAB(2015) Implements WDKA (2015).
   1. Uses phase encoded coherent states
   2. Per half a bit message: Transmission Distance(d)=500 m, Length of the key(L)=$1.93*10^{9}$ for security 0.01%, estimated time to sign ($t$)=20 seconds, channel loss= 2.2 dBkm$^{-1}$ at $\lambda =850m$
3. CAFHSTTABS (2016) Implements modified AWKA (2015)
   1. Uses differential phase shift QKD for QDS
   2. message signing rate= 1 or 2 bits per second for security parameter=0.0001, Length of keys(L)=2Mbits, Transmission distance=90 km, QBER=1.08%, attenuation=0.32 dBkm$^{-1}$
4. CAFHSTTSAB (2017) Implements modified AWKA (2015) using DPS QKD
   1. Per half a bit message: Channel loss=43 dB, transmission distance= 132 km, security parameter=$10^{-4}$
5. YFLTWYZCWZCCP (2018) Implements decoy state QDS scheme in YFC (2016)
   1. Uses nanowire single photon detectors (SNSPD), BB84 state encoding, decoy state modulation.
   2. Signed a 32 bit message "USTC" over transmission distance 102 km, authentication threshold =2%, verification threshold=0.6%, security bound parameter=$10^{-5}$, estimated time=360 seconds for one bit message
6. ZZDZGW (2018) Implements a passive decoy state protocol which uses Passive BB84 Key Generation protocol (KGP) to share public keys from Bob and Charlie to Alice.
   1. Uses parametric down-conversion (PDC) source, secure to coherent attacks
   2. Per half a bit message:Transmission Distance(d)=100 km, QBER(%)=$2.95\%-3.28\%$ for security parameter=$10^{-4}$, attenuation=45.8 dB at 200 km estimated time to sign ($t$)=7 seconds