Secure Multiparty Delegated Classical Computation: Difference between revisions
(Created page with "It provides a method for computing nonlinear multivariable functions using only linear classical computing and limited manipulation of quantum information To demonstrate this...") |
|||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
This [https://arxiv.org/abs/1708.06144 example protocol] provides a method for computing nonlinear functions involving multiple variables using only linear classical computing and limited manipulation of quantum information. | |||
To demonstrate this protocol, the pairwise AND function is computed and can be used as a building block for other functions. | To demonstrate this protocol, the pairwise AND function is computed and can be used as a building block for other functions. | ||
'''Tags:''' [[:Category:Multi Party Protocols|Multi Party Protocols]], [[:Category:Quantum Enhanced Classical Functionality|Quantum Enhanced Classical Functionality]], [[:Category:Universal Task|Universal Task]] | |||
[[Category:Multi Party Protocols]] [[Category:Quantum Enhanced Classical Functionality]][[Category:Universal Task]] | |||
==Assumptions== | ==Assumptions== | ||
| Line 12: | Line 17: | ||
The server sends an ancilla bit to the first client. | The server sends an ancilla bit to the first client. | ||
The first client performs the <math>\pi/2</math> rotation along <math>y</math>-axis according to his input bit and <math>\pi</math> rotation | The first client performs the <math>\pi/2</math> rotation along <math>y</math>-axis according to his input bit and <math>\pi</math> rotation according to his random bit for security. | ||
He then sends the qubit to the next client who performs the same rotation according to his bits. | He then sends the qubit to the next client who performs the same rotation according to his bits. | ||
This process | This process is followed until all clients have performed their operations. | ||
Now, one of the | Now, one of the clients performs the conjugate transpose of the <math>\pi/2</math> rotation on the qubit based on the global XOR of all the inputs which he gets by the XOR routine. | ||
The state now prepared is the value of the function XORed with the XOR of the random bits of all clients. | The state now prepared is the value of the function XORed with the XOR of the random bits of all clients. | ||
The clients now announce the random bits with the help of which the final result is calculated. | The clients now announce the random bits with the help of which the final result is calculated. | ||
| Line 25: | Line 30: | ||
To calculate the global XOR, the send their results to the designated client who then performs the XOR of all the received bits to get the global XOR. | To calculate the global XOR, the send their results to the designated client who then performs the XOR of all the received bits to get the global XOR. | ||
==Notation== | |||
== | |||
* <math>C_i</math>: Client with index <math>i</math>. | * <math>C_i</math>: Client with index <math>i</math>. | ||
| Line 35: | Line 39: | ||
* <math>V</math>: Operator for performing <math>\pi</math> rotation around <math>y</math>-axis in Bloch Sphere. | * <math>V</math>: Operator for performing <math>\pi</math> rotation around <math>y</math>-axis in Bloch Sphere. | ||
==Requirements== | |||
== | |||
* Basic state preparation and measurement devices. | * Basic state preparation and measurement devices. | ||
* Access to secure classical channels. | * Access to secure classical channels. | ||
<br/> | |||
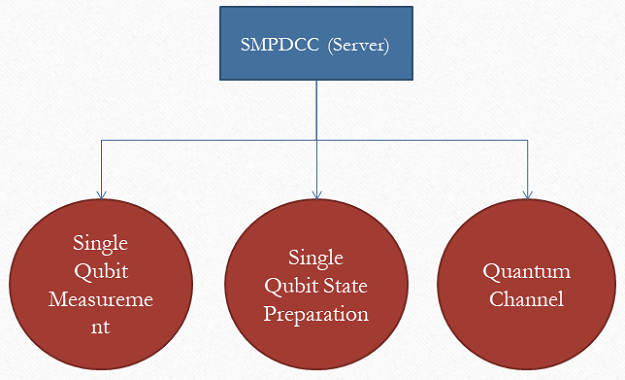
[[File:SMPDCC_Server.PNG|center|Secure Multiparty Delegated Classical Computation (Server)]] | |||
<br/> | |||
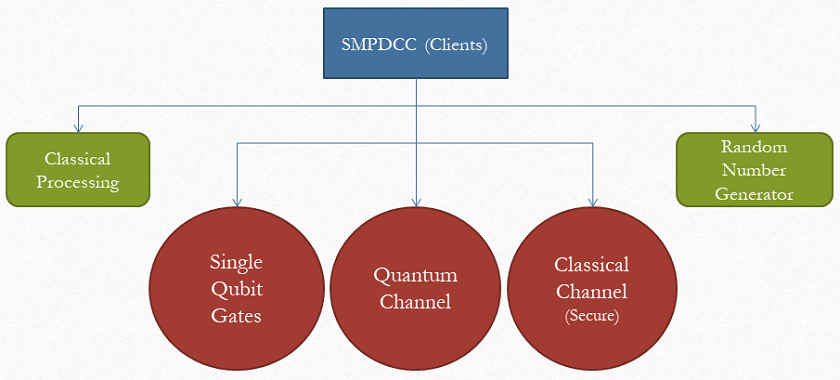
[[File:SMPDCC_Client.PNG|center|Secure Multiparty Delegated Classical Computation (Client)]] | |||
==Properties== | ==Properties== | ||
| Line 49: | Line 59: | ||
== | ==Protocol Description== | ||
To compute <math>f(x_1, x_2,... , x_n) = \Sigma_{i,j = 1}^{n} x_i x_j \forall i \neq j</math>, | To compute <math>f(x_1, x_2,... , x_n) = \Sigma_{i,j = 1}^{n} x_i x_j \forall i \neq j</math>, | ||
| Line 59: | Line 69: | ||
## <math>C_i</math> applies <math>V^{r_i}U^{x_i}</math> on the received qubit and sends it to client <math>C_{i+1}</math>. | ## <math>C_i</math> applies <math>V^{r_i}U^{x_i}</math> on the received qubit and sends it to client <math>C_{i+1}</math>. | ||
# <math>C_n</math> applies <math>V^{r_n}U^{x_n}</math> on the received qubit. | # <math>C_n</math> applies <math>V^{r_n}U^{x_n}</math> on the received qubit. | ||
# Any client then applies <math>(U^\dagger)^{\oplus_i x_i}</math>. | # Any client then applies <math>(U^\dagger)^{\oplus_i x_i}</math>. <br/> <math>(U^\dagger)^{\oplus_i x_i} \underbrace{V^{r_n}U^{x_n}}_{\mathcal{C}_n} ... \underbrace{V^{r_2}U^{x_2}}_{\mathcal{C}_2} \underbrace{V^{r_1}U^{x_1}}_{\mathcal{C}_1} |0\rangle= |r \oplus f\rangle </math> | ||
# The resulting state is now sent to the server who measures the outcome <math>r \oplus f</math> and announces it. | # The resulting state is now sent to the server who measures the outcome <math>r \oplus f</math> and announces it. | ||
# The clients locally compute XOR of the random bits of other clients. | # The clients locally compute XOR of the random bits of other clients. | ||
# They then perform the operation <math>f = r \oplus (r \oplus f)</math> to get the result. | # They then perform the operation <math>f = r \oplus (r \oplus f)</math> to get the result. | ||
===XOR Routine=== | ===XOR Routine=== | ||
| Line 81: | Line 80: | ||
## Each client <math>C_i</math> then computes <math>\tilde{x}_i=\bigoplus_{j=1}^n x_j^i</math> and <math>\tilde{r}_i=\bigoplus_{j=1}^n r_j^i</math>. | ## Each client <math>C_i</math> then computes <math>\tilde{x}_i=\bigoplus_{j=1}^n x_j^i</math> and <math>\tilde{r}_i=\bigoplus_{j=1}^n r_j^i</math>. | ||
# To perform the operation <math>U^\dagger</math>, the clients send <math>\tilde{x}_i</math> to the designated client, who computes the global XOR. <br/> <math> \bigoplus_{i=1}^n x_i=\bigoplus_{i=1}^n \tilde{x}_i </math> | # To perform the operation <math>U^\dagger</math>, the clients send <math>\tilde{x}_i</math> to the designated client, who computes the global XOR. <br/> <math> \bigoplus_{i=1}^n x_i=\bigoplus_{i=1}^n \tilde{x}_i </math> | ||
# When server announces < | # When server announces <math>r \oplus f</math>, all clients broadcast <math>\tilde{r}_i</math> to calculate <math>r</math> and know the value of <math>f</math>. | ||
== Further Information == | |||
<div style='text-align: right;'>''*contributed by Natansh Mathur''</div> | <div style='text-align: right;'>''*contributed by Natansh Mathur''</div> | ||
Latest revision as of 10:51, 16 July 2019
This example protocol provides a method for computing nonlinear functions involving multiple variables using only linear classical computing and limited manipulation of quantum information. To demonstrate this protocol, the pairwise AND function is computed and can be used as a building block for other functions.
Tags: Multi Party Protocols, Quantum Enhanced Classical Functionality, Universal Task
Assumptions[edit]
- The clients have limited computational capabilities, namely access to linear XOR functionalities.
Outline[edit]
Main Routine[edit]
The server sends an ancilla bit to the first client. The first client performs the rotation along -axis according to his input bit and rotation according to his random bit for security. He then sends the qubit to the next client who performs the same rotation according to his bits. This process is followed until all clients have performed their operations. Now, one of the clients performs the conjugate transpose of the rotation on the qubit based on the global XOR of all the inputs which he gets by the XOR routine. The state now prepared is the value of the function XORed with the XOR of the random bits of all clients. The clients now announce the random bits with the help of which the final result is calculated.
XOR Routine[edit]
The clients choose random bits whose XOR is their input bit and send each such random bit to each client. The clients now perform the XOR of the received bits. To calculate the global XOR, the send their results to the designated client who then performs the XOR of all the received bits to get the global XOR.
Notation[edit]
- : Client with index .
- : Input bit of client.
- : Random bit of client.
- : Rotation around -axis in Bloch sphere by angle .
- : Operator for performing rotation around -axis in Bloch Sphere.
- : Operator for performing rotation around -axis in Bloch Sphere.
Requirements[edit]
- Basic state preparation and measurement devices.
- Access to secure classical channels.
Properties[edit]
- The input of each client remains hidden from the other clients and from the server.
- The server performs the computation without learning anything about the result.
- As long as at least two clients are honest, it is enough to guarantee the secrecy of the independent inputs.
Protocol Description[edit]
To compute ,
Main Routine[edit]
- The server generates an ancilla bit and sends it to client .
- For to :
- applies on the received qubit and sends it to client .
- applies on the received qubit.
- Any client then applies .
- The resulting state is now sent to the server who measures the outcome and announces it.
- The clients locally compute XOR of the random bits of other clients.
- They then perform the operation to get the result.
XOR Routine[edit]
- For
- Each client chooses random bits , such that and and sends and to client .
- Each client then computes and .
- To perform the operation , the clients send to the designated client, who computes the global XOR.
- When server announces , all clients broadcast to calculate and know the value of .